Lab 2: Generating random numbers

Discrete probability distributions

In this lab, we will generate random numbers from a probability distribution. We begin with a discrete probability distribution.

x	1	2	3
p	1/3	1/3	1/3

The R function sample() can be used to generate random numbers from a discrete probability distribution. For example, the following code will randomly pick a number from (1,2,3) without replacement

sample(x=1:3, size = 1, replace=FALSE, prob = c(1/3,1/3,1/3))

1

To select two numbers at random from (1,2,3) without replacement, we do

sample(x=1:3, size = 2, replace=FALSE, prob = c(1/3,1/3,1/3))

1. 3
2. 2

To select two numbers at random from (1,2,3) with replacement, we do

sample(x=1:3, size = 2, replace=TRUE, prob = c(1/3,1/3,1/3))

1. 2
2. 1

Exercise 1

Flipping a fair coin 5 times and then we count the number of heads. Suppose head is 1 and tail is 0. Because it is a fair coin, the probability distribution of X is

x	0	1
p	0.5	0.5

outcome = sample(x=c(0,1), size = 5, replace=TRUE, prob=rep(0.5,2))
outcome
print(paste("The count of heads is", sum(outcome)))

1. 1
2. 1
3. 1
4. 0
5. 1

[1] "The count of heads is 4"

Exercise 2

We repeat the above experiment 1000 times and we would like to see how the number of heads varies across 1000 experiments.

nsim = 1000
result = rep(0,nsim)
for(i in 1:nsim){
    outcome = sample(x=c(0,1), size = 5, replace=TRUE, prob=rep(0.5,2))
    result[i] = sum(outcome)
}
table(result)
barplot(table(result))

result
  0   1   2   3   4   5 
 35 154 305 308 156  42 

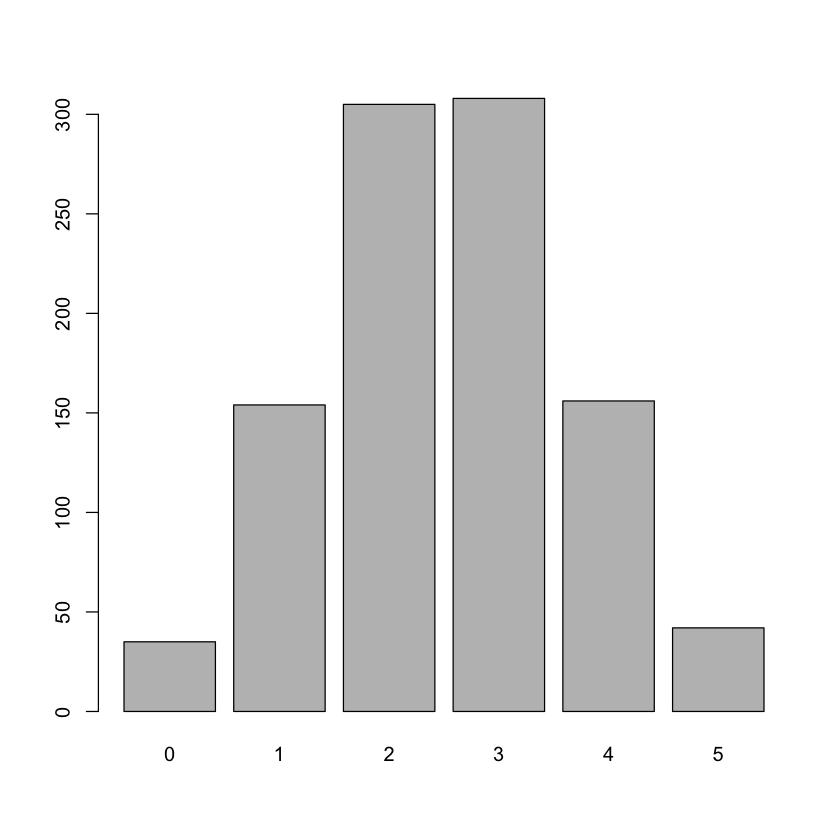
Alternative, we may simulate random numbers from the binomial distribution with \(n=5\) and \(p=0.5\).

result = rbinom(1000,size=5,p=0.5)
table(result)
barplot(table(result))

result
  0   1   2   3   4   5 
 38 167 319 285 159  32 

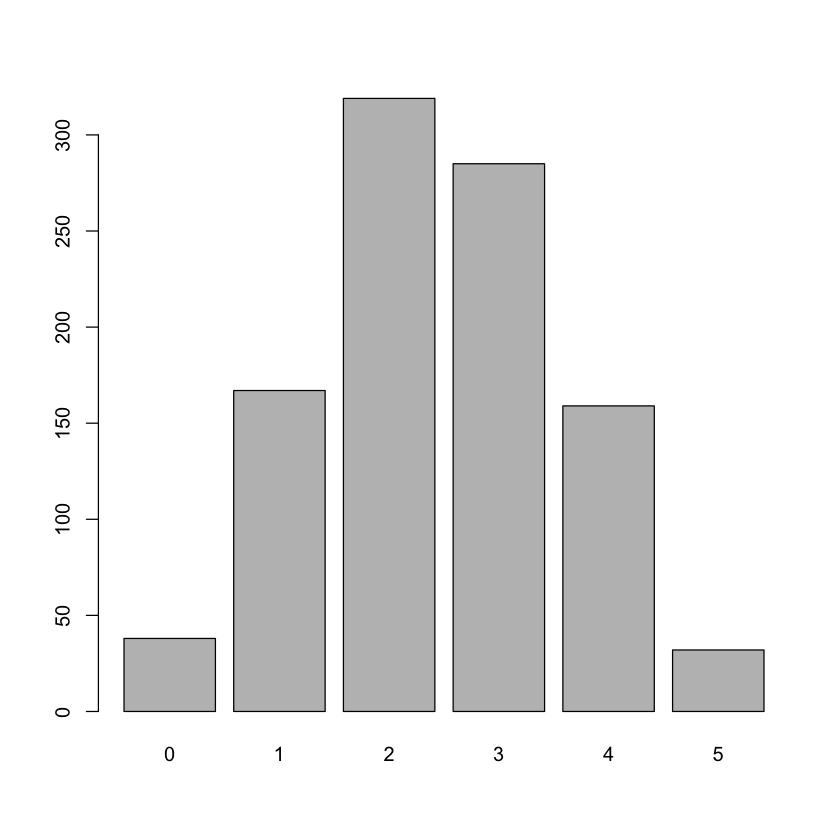
Exercise 3

Given a DNA sequence AGCCCGGGTTTACCCTTGGGAAAATTGCCCCAGTGACCCCT,

1. calculate the proportion of A, C, G, T.

2. Use R to randomly select a nucleotide from the DNA sequence

3. Now we want to select 10 nucleotides without replacement. Then calculate the sample proportions of A, C, G, T among the 10 selected nucleotides and compare them with the population proportions of A, C, G, T in the DNA sequence.

4. Let’s select 100 nucleotides and calculate the sample proportions.

seq = "AGCCCGGGTTTACCCTTGGGAAAATTGCCCCAGTGACCCCT"
x = unlist(strsplit(seq,split=""))

#proportions of A, C, G, T
sum(x=='A')/length(x)
sum(x=='C')/length(x)
sum(x=='G')/length(x)
sum(x=='T')/length(x)

#select a nucleotide
position=sample(1:length(x),size=1)
x[position]

#sample 10 nucleotides without replacement
position = sample(1:length(x),size=10)
data = x[position]
data
print("the proportions of A, C, G, T in the sample of 10 nucleotides")
sum(data=='A')/10
sum(data=='C')/10
sum(data=='G')/10
sum(data=='T')/10

#sample 100 nucleotides with replacement
position = sample(1:length(x),size=100,replace=TRUE)
data = x[position]
print("the proportions of A, C, G, T in the sample of 100 nucleotides")
sum(data=='A')/100
sum(data=='C')/100
sum(data=='G')/100
sum(data=='T')/100

0.195121951219512

0.341463414634146

0.24390243902439

0.219512195121951

'C'

1. 'A'
2. 'C'
3. 'T'
4. 'A'
5. 'C'
6. 'T'
7. 'G'
8. 'C'
9. 'C'
10. 'C'

[1] "the proportions of A, C, G, T in the sample of 10 nucleotides"

0.2

0.5

0.1

0.2

[1] "the proportions of A, C, G, T in the sample of 100 nucleotides"

0.19

0.36

0.23

0.22

To generate a random number from the binomial distribution

rbinom(n=10, size=5, prob=0.5)

1. 2
2. 3
3. 3
4. 2
5. 2
6. 4
7. 3
8. 2
9. 3
10. 2

to generate a random number from the Poisson distribution

rpois(n=10, lambda=3.5)

1. 6
2. 3
3. 4
4. 1
5. 3
6. 3
7. 0
8. 3
9. 3
10. 4

Continuous probability distributions

We may generate a random number from an interval [a, b] using the R function runif(). For example, we may generate a random number between 0 and 2,

runif(1, min=0, max=2)

1.94677625317127

Or generate 10 random numbers from the interval [2, 10]

runif(10, min=2, max=10)

1. 3.23496624082327
2. 7.76770966872573
3. 5.36018450558186
4. 2.4951937533915
5. 9.52136170677841
6. 4.55617613531649
7. 8.0581475533545
8. 8.49363647028804
9. 2.55170818045735
10. 2.27868529781699

We may generate 10 random numbers from the normal distribution with mean = 4.5 and variance = 2 and then calculate the sample average.

data = rnorm(10, mean=4.5, sd=sqrt(2))
data
print(paste("the sample average:",mean(data)))

1. 4.5062229924065
2. 5.11821511476538
3. 3.14321250263959
4. 5.72484443164852
5. 3.73176494917267
6. 4.36132261330203
7. 5.81746174114681
8. 8.10412427773735
9. 7.0695020475563
10. 7.29412543343412

[1] "the sample average: 5.48707961038093"

Dealing with sequence files

The R function scan() can read text files into R. FASTA format: A sequence record in a FASTA format consists of a single-line description (sequence name), followed by line(s) of sequence data. The first character of the description line is a greater-than (“>”) symbol. To read FASTA file test.fasta, the R code is

x = scan("https://book.phylolab.net/binf8441/data/lab2_test.fasta", what="character",sep="\n")

Then, we count the number of sequences in the file. In addition, what is the length of those sequences. Also, calculate the proportion of A, C, G, T in each sequence.

#count the number of >
index = grep(">",x)
nseq = length(index)
print(paste("the number of sequences:",nseq))

#get sequences
seq=rep("",length(index))
for(i in 1:length(index)){
    if(i < length(index)){
        seq[i] = paste(x[(index[i]+1):(index[i+1]-1)],collapse="",sep="")
    }else{
        seq[i] = paste(x[(index[i]+1):length(x)],collapse="",sep="")
    }
}

#sequence length
seqlength = nchar(seq[1])
print(paste("the sequence length is",seqlength))

#proportions
prop = matrix(0,nrow=nseq,ncol=4)
row.names(prop) = paste("seq",1:nseq,sep="")
for(i in 1:nseq){
    s = unlist(strsplit(seq[i],split=""))
    prop[i,] = c(sum(s=='a'), sum(s=='c'), sum(s=='g'), sum(s=='t'))/seqlength
}
print("the proportions of a, c, g, t in each sequence")
prop

[1] "the number of sequences: 5"

[1] "the sequence length is 279"

[1] "the proportions of a, c, g, t in each sequence"

A matrix: 5 × 4 of type dbl

seq1	0.1792115	0.1648746	0.1505376	0.3225806
seq2	0.1505376	0.1505376	0.1433692	0.3010753
seq3	0.1720430	0.1648746	0.1541219	0.3261649
seq4	0.2329749	0.1075269	0.1648746	0.3225806
seq5	0.2258065	0.1039427	0.1648746	0.3333333