Chapter 15: Phylogenetic models#

“Do the difficult things while they are easy and do the great things while they are small. A journey of a thousand miles must begin with a single step.”

—Lao Tzu

See also

The probability distribution of the sequence alignment \(D\) given the phylogenetic tree \(T\) (topology and branch lengths) and the parameters \(\theta\) in the substitution model can be derived from the transition probabilities \(P(t)=e^{Qt}\) of the substitution model.

We assume that the sequences have been aligned using alignment software (Clustal, MUSCLE, MAFFT), and the sites in the sequence alignment evolve independently. The joint probability of the alignment \(D\) is the product of the probabilities of individual sites \(d_i\)

\[P\left( D|T,\theta \right) = \prod_{i = 1}^{n}{P(d_{i}|T,\theta)}\]

in which \(P(d_{i}|T)\) is the probability of the site \(d_i\). In the phylogenetic model, parameters being estimated include the phylogenetic tree \(T\) (topology and branch lengths) and parameters \(\theta\) in the substitution model.

The probability of a single site#

Considering the site \(d_i = (A, C, A)\) in figure (a). If the nucleotides at the internal nodes are given, then the probability of figure (b) is the product of probabilities for individual branches, i.e.,

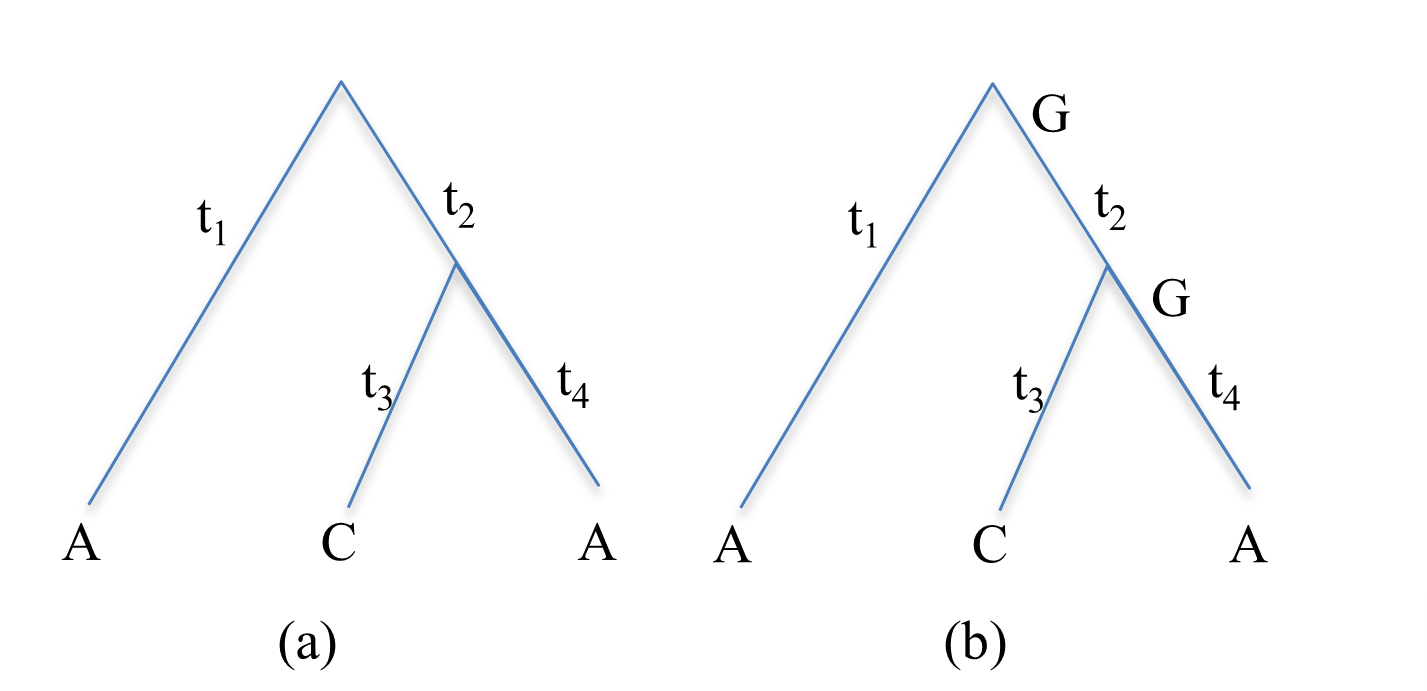
\[P\left(ACAGG \right) = P(G)P_{GA}(t_{1})P_{GG}(t_{2})P_{GC}(t_{3})P_{GA}(t_{4})\]

Thus, the probability of the site \(d_i = (A, C, A)\) is equal to the sum over all possible nucleotides at the two internal nodes, i.e.,

\[P\left( d_{i} \middle| T,\theta \right) = \sum_{i = A,C,G,T}^{}{\sum_{j = A,C,G,T}^{}{P(ACAij)}}\]

in which \(P(ACAij)\) denotes the probability when the nucleotides at the two internal nodes are \(i\) and \(j\).

Maximum likelihood tree#

The phylogenetic tree is estimated by maximizing the likelihood function \(L\left( T,\theta|D \right) = P\left( D|T,\theta \right) \) with respect to \(T\) and \(\theta\). RAxML and PHYML are two popular phylogenetic programs for building ML phylogenetic trees.

Distance methods#

Phylogenetic trees are constructed by iteratively grouping species based on small distances. Distance methods typically involve two steps. In the initial step, pairwise distances between sequences are computed. Subsequently, in the second step, the phylogenetic tree is constructed using these pairwise distances. One of the most widely used distance methods is neighbor-joining (NJ), implemented in various phylogenetic programs. PAUP.

Parsimony methods#

The parsimony score of a phylogenetic tree corresponds to the number of mutations needed to account for the observed nucleotide variation among sequences. Parsimony methods for reconstructing phylogenetic trees aim to minimize the parsimony score, essentially seeking the tree with the lowest possible parsimony score. PAUP is a popular program for building MP trees

Bayesian models#

The tree topology is assigned a uniform prior, assuming equal likelihood for all topologies. Branch lengths have independent exponential distributions as their priors. The posterior distribution of the phylogenetic tree is approximated using the outputs from a Markov Chain Monte Carlo (MCMC) algorithm. Bayesian phylogenetic programs that implement this approach include: MrBayes and BEAST.