Chapter 1: Probability theory#
“Do the difficult things while they are easy and do the great things while they are small. A journey of a thousand miles must begin with a single step.”
—Lao Tzu
See also
Probability Axioms
Probability is a real number between 0 and 1
The total probability is 1
Countable addition: For the disjoint events \(E_{1}, E_{2}, \ldots\), the probability of the union is equal to the sum of the probabilities of individual events, i.e.,
The union \(A\cup B\) of two events \(A\) and \(B\) denotes that either \(A\) or \(B\) or both occur.
The intersection \(A\cap B\) of two events \(A\) and \(B\) denotes that both \(A\) and \(B\) occur.
The complement \(\bar{A}\) of \(A\) denotes not \(A\)
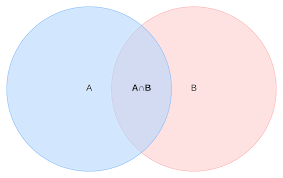
Calculating probabilities#
\(P(\bar{A})=1-P(A)\)
\(P(A\cup B) = P(A)+P(B)-P(A\cap B)\)
If two events \(A\) and \(B\) are disjoint, then \(P(A\cap B) = 0\)
Example 1
Flipping a coin, the probabiliy of a head is 0.47. What is the probability of a tail?
\(P(tail) = 1-P(head) = 1-0.47 = 0.53\)
Example 2 (1.2)
Find the probability of a head or a tail?
\(P(head \cup tail) = P(head) + P(tail) - P(head\cap tail) = 0.47 + 0.53 - 0 = 1\)
Conditional probabilities#
Definition 1 (conditional probability)
For two events \(A\) and \(B\), the probability of \(A\) given that the event \(B\) occurs is called the conditional probability of \(A\) conditional on the event \(B\), denoted by \(P(A|B)\).
\(P(A|B)=\frac{P(A \cap B)}{P(B)}\)
\(P(A\cap B) = P(A)P(B|A) = P(B)P(A|B)\)
Example 3
Show that if A is a subset of B, then \(P(B|A) = 1\)
\(P(B|A)=\frac{P(A \cap B)}{P(A)}=\frac{P(A)}{P(A)}=1\)

Example 4
John has an 80% probability of having dinner at home and a 20% probability of dining at a restaurant. If he opts for a home-cooked meal, there’s a 40% chance he’ll choose chicken and a 60% chance he’ll choose vegetables. On the other hand, if he dines at a restaurant, there’s a 90% probability he’ll choose chicken and a 10% probability he’ll choose vegetables. (see the diagram)
Let \(H=home\), \(R=restaurant\), \(C=chicken\), and \(V=veg\). From the diagram, we know that \(P(H)=0.8\), \(P(R=0.2)\), \(P(C|H)=0.4\), \(P(V|H)=0.6\), \(P(C|R)=0.9\), \(P(V|R)=0.1\).
What is the probability of having chicken at home? \(P(H \cap C) = P(C|H)P(H) = 0.4\times 0.8 = 0.32\)
What is the probability of having chicken? \(P(C) = P(C\cap H)+P(C\cap R) = P(C|H)P(H)+P(C|R)P(R) = 0.4\times 0.8 + 0.9\times 0.2 = 0.32+0.18=0.5\)
If John is having chicken, what is the probability that he is having chicken at home? \(P(H|C) = \frac{P(H\cap C)}{P(C)} = \frac{0.4\times 0.8}{0.5} = 0.64\)
Independent events#
Definition 2 (independence)
Two sets (events) \(A\) and \(B\) are independent if and only if \(P(A \cap B)=P(A) P(B)\).
Example 5
Show that if two event A and B are independent of each other, then \(P(A|B) = P(A)\)
By definition, the conditional probability is \(P(A|B) = \frac{P(A\cap B)}{P(B)}\). Since \(A\) and \(B\) are independent, \(P(A\cap B) = P(A)P(B)\). Thus, \(P(A|B) = \frac{P(A)P(B)}{P(B)} = P(A)\)
Example 6
Show that two disjoint events A and B with positive probabilities, i.e., \(P(A)>0\) and \(P(B)>0\), must be dependent of each other.
We show it by contradiction. Suppose \(A\) and \(B\) are independent. Then, \(P(A\cap B) = P(A)P(B)>0\). However, \(A\) and \(B\) are disjoint and thus \(P(A\cap B) = 0\).
Example 7
Let \(X_1, X_2, X_3\) be the outcomes of three flips. Find the probability of three heads.
Because three flips are independent of each other, the probability of three heads is equal to the product of the probablities of individual flips.
