Lab 11: Bootstrap#

Suppose \(x_1, \ldots, x_{10} \sim \operatorname{Normal}\left(\mu, \sigma^2\right)\). Let \(\hat{\mu}\) be an estimator of \(\mu\). It could be the sample mean, sample median, maximum likelihood estimator, or any point estimator. We will calculate \(\operatorname{var}(\hat{\mu})\) using bootstrap samples.

data = rnorm(10, mean=4, sd=2)
sample_median = median(data)
sample_median
3.63888684062208

Parametric bootstrap:#

We estimate the unknown parameters, \(\hat{\mu}_{MLE}=\bar{x}\) and \(\widehat{\sigma^2}_{MLE}=\) sample variance

mu_hat = mean(data)
var_hat = var(data)

Generate \(k\) bootstrap samples from the \(Normal(\hat{\mu}_{MLE}, \widehat{\sigma^2}_{MLE})\)

k=100
bootstrap_sample = matrix(0, nrow=10, ncol=k)
for(i in 1:k){
  bootstrap_sample[,i] = rnorm(10, mean=mu_hat, sd=sqrt(var_hat))
}

Calculate \(\hat{\mu}\), i.e., the sample median for each bootstrap sample, \(\left\{\widehat{\mu_1}, \ldots, \widehat{\mu_k}\right\}\)

sample_median = 1:k
for(i in 1:k){
  sample_median[i] = median(bootstrap_sample[,i])
}
sample_median
  1. 4.44561786211302
  2. 4.67772682829274
  3. 3.95971029518667
  4. 3.56429335057606
  5. 3.22791076964354
  6. 4.15631415003103
  7. 3.55784257266926
  8. 3.90550150781958
  9. 3.09007472701129
  10. 4.91897524350442
  11. 4.32535237723643
  12. 4.83223639815947
  13. 4.46929668959023
  14. 3.69511283713728
  15. 2.68855557754801
  16. 2.85140838060864
  17. 3.03506042277317
  18. 4.20334173000931
  19. 3.95512806553804
  20. 2.65923691897263
  21. 3.02682707800827
  22. 3.59143334776439
  23. 2.38390048928055
  24. 4.32231456459515
  25. 4.27343965067856
  26. 2.82692356258043
  27. 3.65473106342307
  28. 3.73188321927561
  29. 3.42709245173773
  30. 4.10427914767153
  31. 4.77495513029408
  32. 3.90674431199055
  33. 3.35159200455574
  34. 3.64528696398739
  35. 3.59144224138914
  36. 3.07424947805679
  37. 4.30598955667739
  38. 5.00962542529426
  39. 3.34764937395769
  40. 4.84854483747192
  41. 4.00925426768146
  42. 3.65788344395059
  43. 3.84512184008322
  44. 3.53713712767478
  45. 3.92167018089209
  46. 4.09844644374319
  47. 4.1038718403586
  48. 4.84581570094966
  49. 3.73743228530132
  50. 3.16548900622553
  51. 4.64148149593731
  52. 4.26678621069261
  53. 4.29102920733568
  54. 3.62127507443068
  55. 4.51414046741928
  56. 3.84800778802832
  57. 4.06587792244641
  58. 3.76486361672103
  59. 6.09200255403587
  60. 4.54743151520859
  61. 4.16831492675626
  62. 5.07621692973946
  63. 3.11781527924284
  64. 3.95615444325829
  65. 3.74621514553175
  66. 2.28505367529484
  67. 3.48134342791253
  68. 4.13755312369523
  69. 3.82767134390163
  70. 4.45827013923297
  71. 3.07662842476346
  72. 4.32525384294122
  73. 3.8522838159386
  74. 3.91783324019871
  75. 3.52846183603836
  76. 4.20205670992562
  77. 6.24415787739707
  78. 4.64662440415347
  79. 5.56005877102173
  80. 5.03235312377744
  81. 4.26968603062587
  82. 3.98168382038422
  83. 4.35175979853733
  84. 3.81066799440101
  85. 4.8246774926414
  86. 4.05818113591943
  87. 1.8942930720193
  88. 3.82179482277564
  89. 2.98054417735195
  90. 3.92967338842795
  91. 3.78697098031984
  92. 2.10136549471903
  93. 3.90641814272161
  94. 2.79860689429251
  95. 2.99086868777596
  96. 4.5347050847945
  97. 4.58846317460145
  98. 5.29011608139473
  99. 3.62915624213097
  100. 3.75564981709219

Calculate the sample variance \(S^2\) of \(\left\{\widehat{\mu_1}, \ldots, \widehat{\mu_k}\right\}\), i.e., \(\frac{1}{k-1} \sum_{i=1}^k\left(\widehat{\mu_i}-\widehat{\mu}\right)^2\) and \(\operatorname{var}(\hat{\mu}) \approx S^2\)

var(sample_median)
0.587977762488399

Nonparametric bootstrap#

We generate bootstrap samples by resampling the original data with replacement.

bootstrap_sample = matrix(0, nrow=10, ncol=k)
for(i in 1:k){
  bootstrap_sample[,i] = sample(data,10,replace=T)
}

We calculate the sample median for each bootstrap sample

sample_median = 1:k
for(i in 1:k){
  sample_median[i] = median(bootstrap_sample[,i])
}
sample_median
  1. 4.00634354968367
  2. 3.63888684062208
  3. 4.19995026619835
  4. 4.00634354968367
  5. 4.39355698271303
  6. 2.32418829962678
  7. 3.16526592465523
  8. 4.19995026619835
  9. 5.49068418836301
  10. 3.2714301315605
  11. 2.79780921559364
  12. 3.63888684062208
  13. 3.08379133471808
  14. 2.71650192859014
  15. 3.2714301315605
  16. 3.2714301315605
  17. 2.16157372561978
  18. 3.16526592465523
  19. 4.00634354968367
  20. 3.2714301315605
  21. 4.00634354968367
  22. 3.2714301315605
  23. 2.71650192859014
  24. 2.32418829962678
  25. 3.16526592465523
  26. 4.00634354968367
  27. 2.79780921559364
  28. 3.16526592465523
  29. 4.39355698271303
  30. 3.2714301315605
  31. 2.16157372561978
  32. 3.63888684062208
  33. 3.63888684062208
  34. 3.16526592465523
  35. 2.79780921559364
  36. 4.92962076278674
  37. 3.2714301315605
  38. 6.58781139401298
  39. 5.49068418836301
  40. 6.58781139401298
  41. 2.32418829962678
  42. 4.00634354968367
  43. 2.32418829962678
  44. 5.49068418836301
  45. 3.63888684062208
  46. 4.00634354968367
  47. 3.16526592465523
  48. 2.71650192859014
  49. 6.58781139401298
  50. 2.79780921559364
  51. 3.63888684062208
  52. 3.2775653541664
  53. 4.19995026619835
  54. 5.29707747184833
  55. 3.63888684062208
  56. 2.79780921559364
  57. 5.49068418836301
  58. 4.00634354968367
  59. 6.58781139401298
  60. 2.32418829962678
  61. 3.2714301315605
  62. 6.58781139401298
  63. 3.16526592465523
  64. 4.00634354968367
  65. 5.49068418836301
  66. 2.24288101262328
  67. 3.63888684062208
  68. 5.49068418836301
  69. 2.24288101262328
  70. 4.39355698271303
  71. 3.63888684062208
  72. 4.39355698271303
  73. 3.63888684062208
  74. 4.19995026619835
  75. 4.00634354968367
  76. 4.39355698271303
  77. 2.32418829962678
  78. 3.2714301315605
  79. 6.58781139401298
  80. 2.24288101262328
  81. 3.63888684062208
  82. 3.63888684062208
  83. 3.3588726411699
  84. 6.58781139401298
  85. 3.16526592465523
  86. 5.49068418836301
  87. 4.39355698271303
  88. 2.24288101262328
  89. 3.63888684062208
  90. 6.58781139401298
  91. 4.92962076278674
  92. 4.19995026619835
  93. 2.79780921559364
  94. 5.03321138387595
  95. 3.83249355713676
  96. 3.63888684062208
  97. 2.32418829962678
  98. 3.2714301315605
  99. 6.69140201510219
  100. 5.49068418836301

We calculate the sample variance \(S^2\) of \(\left\{\widehat{\theta_1}, \ldots, \widehat{\theta_k}\right\}\), i.e., \(\frac{1}{k-1} \sum_{i=1}^k\left(\widehat{\theta_t}-\widehat{\theta}\right)^2\) and \(\operatorname{var}(\hat{\theta}) \approx S^2\)

var(sample_median)
1.51156633100485

Building bootstrap phylogenetic trees#

We build a distance phylogenetic tree using the DNA alignment in test.phy.

library(phybase)
data = read.dna.seq("./data/lab15_primates.phy",format="phylip")
seq = data$seq
d = dist.dna(seq)
rownames(d) = data$name
plot(nj(d))

Loading required package: ape

Loading required package: Matrix

Attaching package: ‘phybase’

The following objects are masked from ‘package:ape’:

    dist.dna, node.height
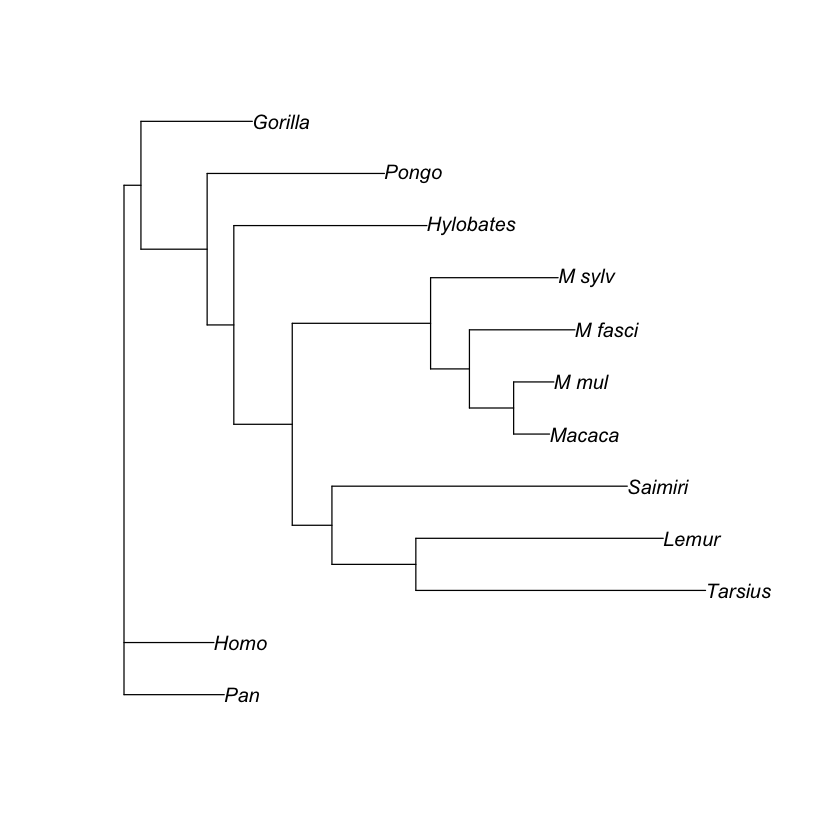
_images/4153650cc79ef8ec5c7f7e00b9f033d1be172099111b543fe15243fe4ed88f79.png

We generate 100 nonparametric boostrap samples, i.e., resampling columns of the DNA alignment with replacement. Then, we build a tree for each bootstrap sample.

ncol = dim(seq)[2]
nbootstrap = 100
bootstrap_tree = rep("",nbootstrap)

for(i in 1:nbootstrap){
  columns = sample(1:ncol,ncol,replace=T)
  bootstrap_sample = seq[,columns]
  d = dist.dna(bootstrap_sample)
  rownames(d) = data$name
  bootstrap_tree[i] = write.tree(nj(d))
}

trees = read.tree(text=bootstrap_tree)
trees

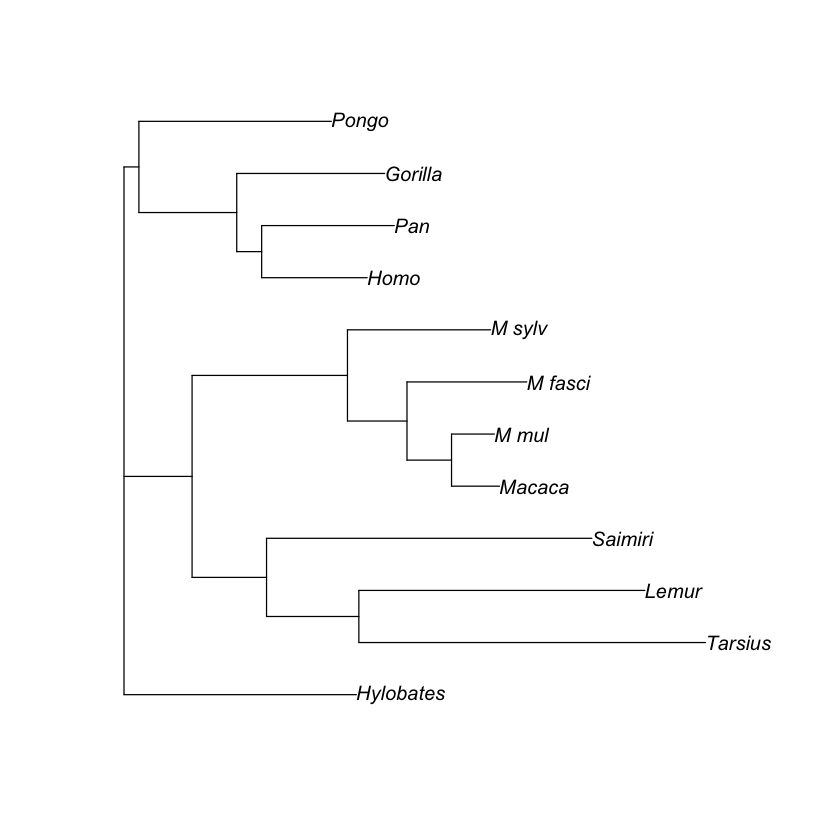
plot(trees[1])
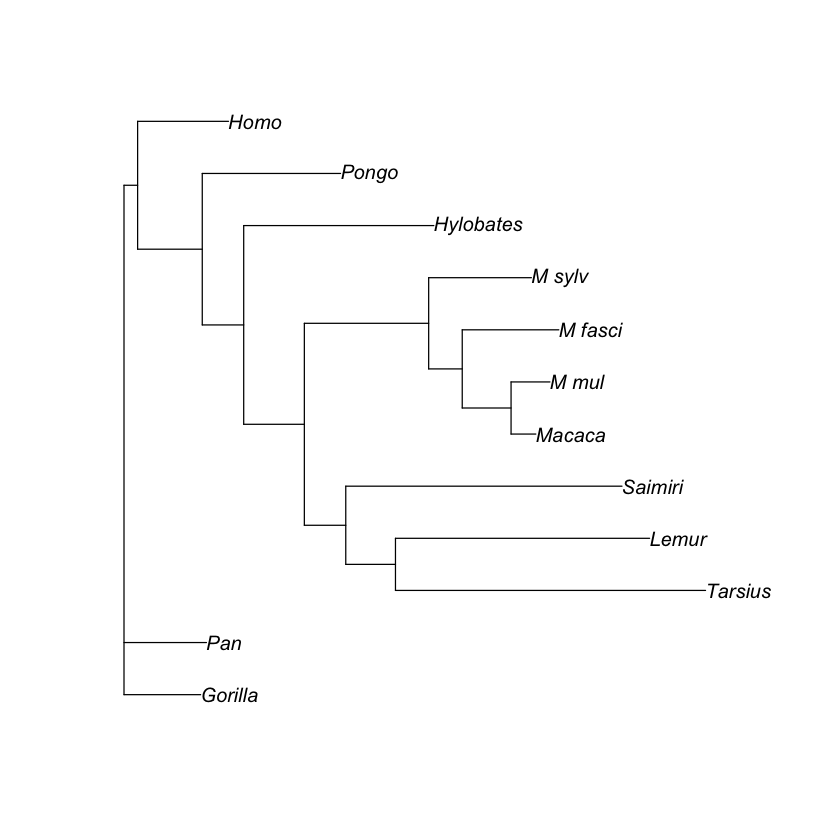
plot(trees[2])
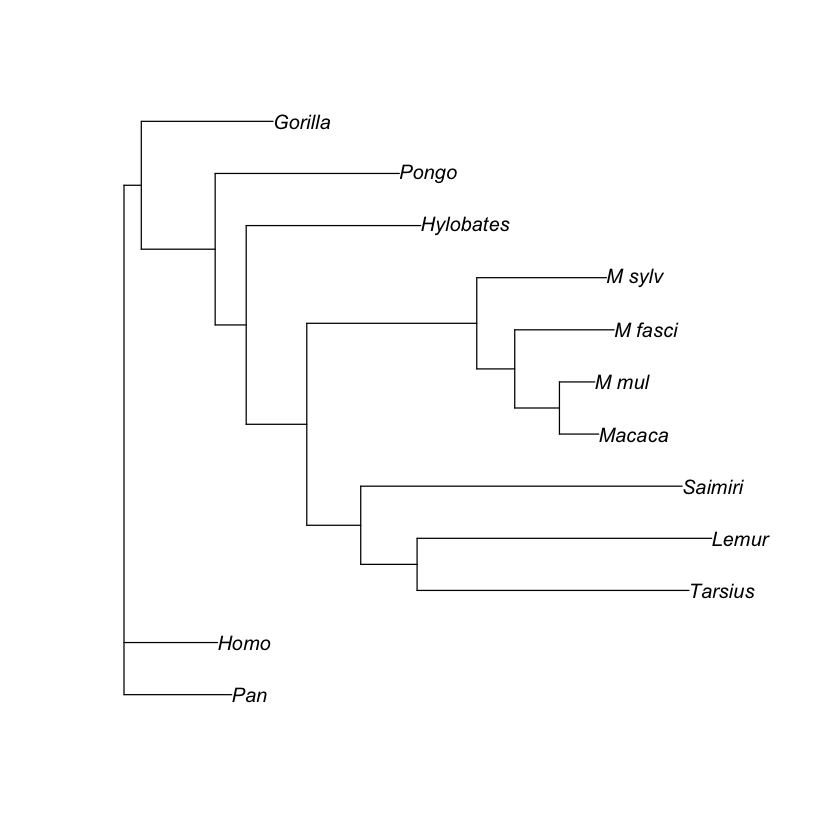
plot(trees[3])
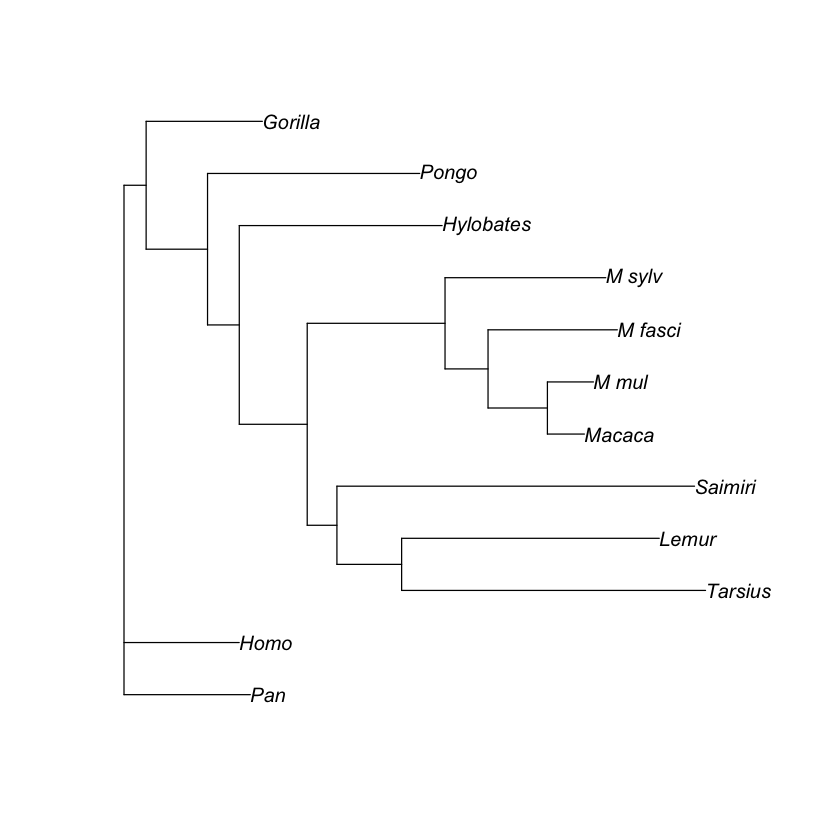
plot(trees[4])

100 phylogenetic trees
_images/47bcb539279980949ce9113986b6ea2ab37254e7b1d9d8a25d698be9f574693c.png _images/9016fd0a37cbedd5c83062cc8949dd8e7e50e32c98d9f909971b2d1016c61979.png _images/2149829c66e10780639ac4c8b2c89028850439a02ff5f7f902ff39f4142ae9f8.png _images/79f9635b0aa0ea2b86318194576706e8cc1f62efc6dcef03022fca68565c32f4.png