Lab 3: Multivariate Methods#

Parameter Estimation#

Let \(𝑋={𝑋_1,…,𝑋_𝑃}\) be a \(p\)-dimension point. The mean vector is \(\mu=𝐸(𝑋)\) and the covariance matrix is \(Σ_{𝑝×𝑝}\)

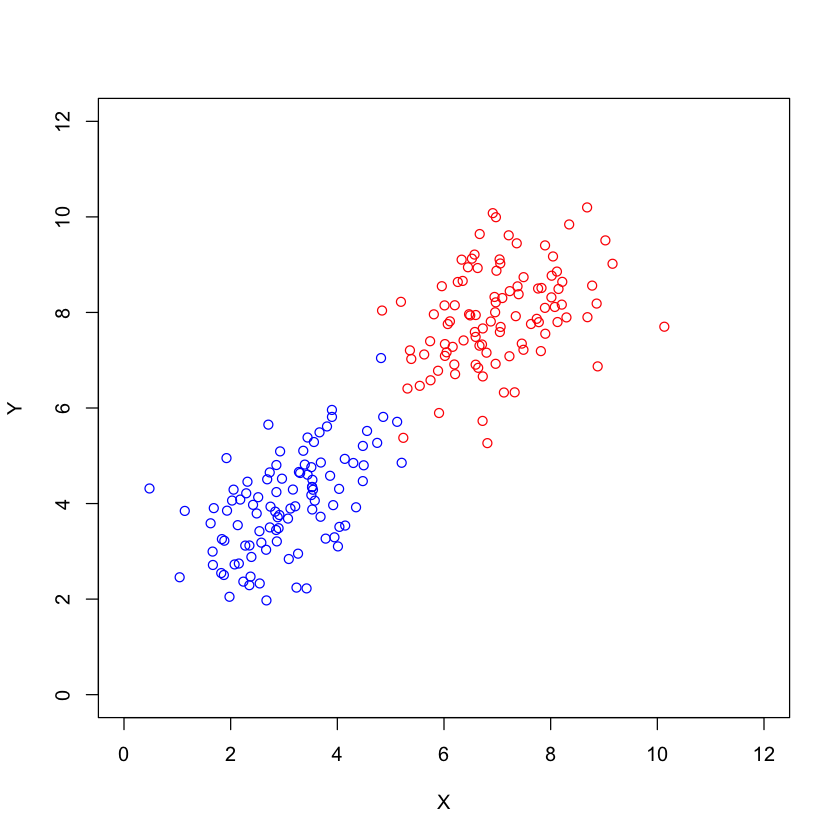
Two normal distributions with different mean and covariance matrix#

library(MASS)
sigma1 = matrix(2,2,2)
sigma1[1,2] = sigma1[2,1]=0.5
bvn1 = mvrnorm(100, mu=c(3,4), Sigma=sigma1)

sigma2 = matrix(1,2,2)
sigma2[1,2] = sigma2[2,1] = 0.5
bvn2 = mvrnorm(100, mu=c(7,8), Sigma=sigma2)

plot(bvn1,xlim=c(0,12),ylim=c(0,12),col="blue",xlab="X",ylab="Y")
points(bvn2,col="red")
_images/3dacae72b44bc9cc6a078e0cd51e1fc147471c5f9a383ab8175569d436172a23.png

The mean vector \(\mu\) can be estimated by the sample average

bvn1_average = apply(bvn1,2,mean)
bvn2_average = apply(bvn2,2,mean)
print("the first group")
bvn1_average
print("the second group")
bvn2_average

[1] "the first group"
  1. 2.87161703821864
  2. 3.94169121104734
[1] "the second group"
  1. 7.11777570362168
  2. 7.99345609581267

The covariance matrix can be estimated by the sample covariance matrix

bvn1_cov = cov(bvn1)
bvn2_cov = cov(bvn2)

print("the first group")
bvn1_cov
print("the second group")
bvn2_cov

[1] "the first group"
A matrix: 2 × 2 of type dbl
2.11317420.3302313
0.33023131.7735052
 
[1] "the second group"
A matrix: 2 × 2 of type dbl
0.90372200.2699806
0.26998060.8289249

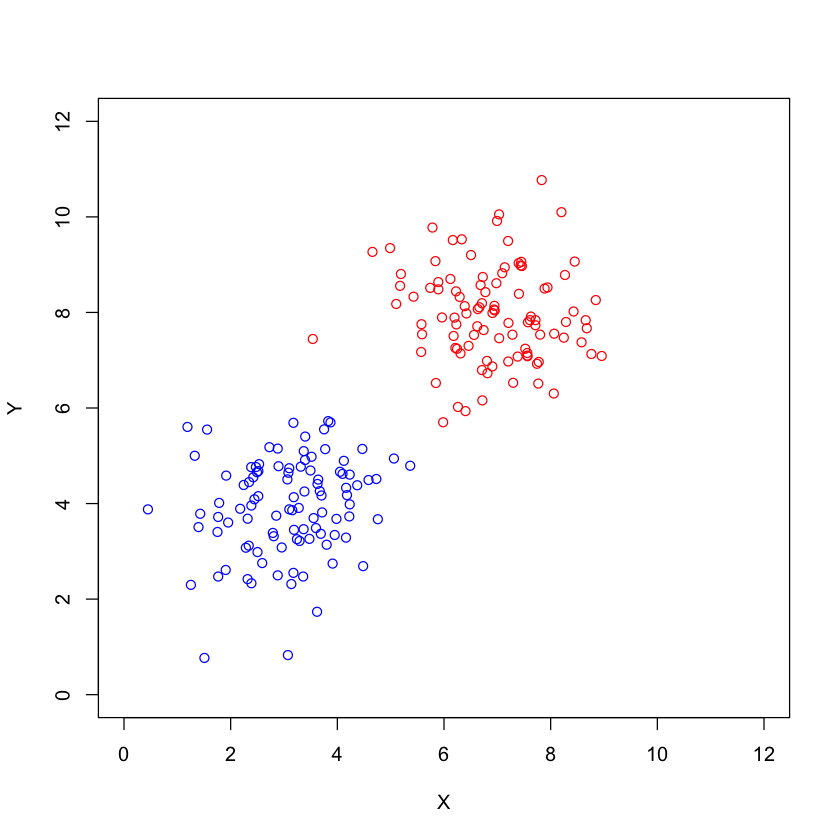
Two classes may have a common covaraince matrix#

sigma = matrix(1,2,2)
sigma[1,2] = sigma[2,1]=0.5

bvn1 = mvrnorm(100, mu=c(3,4), sigma)
bvn2 = mvrnorm(100, mu=c(7,8), sigma)

plot(bvn1,xlim=c(0,12),ylim=c(0,12),col="blue",xlab="X",ylab="Y")
points(bvn2,col="red")
_images/92522c7f5a4f230ac0894665585368c6486aa4f4ae477ac840dd5247dc96c026.png

The covariance matrix is estimated by the sample covariance of the pooled data

pooldata = rbind(bvn1-mean(bvn1),bvn2-mean(bvn2))
bvn1_cov = cov(pooldata)

print("The pooled covariance matrix")
bvn1_cov

[1] "The pooled covariance matrix"
A matrix: 2 × 2 of type dbl
0.94756370.4548899
0.45488991.0334350

Diagnal covariance matrix#

In this case, the coordinate random variables \(X_1,...X_p\) are independently distributed with a normal distribution

sigma = matrix(1,2,2)
sigma[1,2] = sigma[2,1]= 0
sigma[2,2] = 4

bvn1 = mvrnorm(100, mu=c(3,4), sigma)
bvn2 = mvrnorm(100, mu=c(7,8), sigma)

plot(bvn1,xlim=c(0,12),ylim=c(0,12),col="blue",xlab="X",ylab="Y")
points(bvn2,col="red")
_images/6f9fdf00465879642b9920021b8061ca7b5f200b4e4fa1468284feb95c0c79cd.png

Independent random variables with a common variance#

sigma = matrix(1,2,2)
sigma[1,2] = sigma[2,1]= 0

bvn1 = mvrnorm(100, mu=c(3,4), sigma)
bvn2 = mvrnorm(100, mu=c(7,8), sigma)

plot(bvn1,xlim=c(0,12),ylim=c(0,12),col="blue",xlab="X",ylab="Y")
points(bvn2,col="red")
_images/be3203d6f04e4c6ae090c5eefe9d7e5bf6ad964b978acd856f71801c27cd4c9b.png

Estimation of Missing Values#

Values of certain variables may be missing in data. For example, the first 10 values of the first column of bvn1 are missing

bvn1[1:10,1] = NA
bvn1
Hide code cell output
A matrix: 100 × 2 of type dbl
NA3.342038
NA5.142741
NA4.449138
NA3.683020
NA4.620892
NA4.383494
NA3.983260
NA4.329717
NA3.719771
NA3.890577
4.16204463.286794
2.42384734.550390
1.91598404.585138
3.31447634.771536
2.24447114.388768
3.79976883.138331
3.09899023.879268
4.23205454.605499
0.44876723.878384
4.73142054.514621
3.18315264.133918
2.47392744.764042
2.79140913.385800
4.48370582.690229
3.77261705.139406
3.62778934.410551
2.59157362.754170
4.22501903.730195
3.69030953.366985
1.76575102.472587
⋮⋮
1.7841634.0136187
3.1548253.8608814
3.1875523.4497028
4.7598203.6720317
4.1218904.8942886
2.5177724.1546984
3.0732660.8286488
3.4762633.2605749
3.7518185.5526505
1.5578065.5481571
3.4961604.6919553
2.8973654.7821198
3.8288485.7259362
3.9833463.6790456
3.3975735.4021710
3.3591942.4725090
2.3173472.4182551
3.7146643.8142191
4.1809934.1766792
3.9116232.7437576
3.2920953.2170732
3.1765025.6899334
3.3943054.9115720
1.9072262.6100076
2.7260915.1797545
4.0497584.6647227
3.0828374.6455573
3.6198451.7354289
1.5076480.7690181
2.3846714.7626383

We fill in the missing entries by estimating them, i.e., imputation. In the main imputation, missing values are replaced by the average of the available data

bvn1[1:10,1] = mean(bvn1[,1],na.rm=T)
bvn1[1:10,1]
  1. 3.05401879991298
  2. 3.05401879991298
  3. 3.05401879991298
  4. 3.05401879991298
  5. 3.05401879991298
  6. 3.05401879991298
  7. 3.05401879991298
  8. 3.05401879991298
  9. 3.05401879991298
  10. 3.05401879991298

In imputation by regression, missing values are predicted by linear regression

x = bvn1[-(1:10),]
reg = lm(x[,1]~x[,2])
bvn1[1:10,] = reg$coef[1]+bvn1[1:10,2]*reg$coef[2]
bvn1[1:10,1]
  1. 2.96677099935777
  2. 3.23452732602819
  3. 3.13139174297157
  4. 3.01747345299547
  5. 3.15693075435671
  6. 3.12163079969472
  7. 3.06211776135899
  8. 3.1136344182391
  9. 3.02293823082497
  10. 3.04833624202013

Multivariate Classification#

Let \(\{C_i: i=1,...,k\}\) be the \(k\) classes. The points in the class \(C_i\) follow the multivariate normal distribution with mean vector \(\mu_i\) and covariance matrix \(\Sigma_i\).

Given the training data \(X_i\) in class \(C_i\), the mean vector and covariance matrix can be estimated by the sample average \(\bar{X}_i\) and sample covariance matrix \(S_i\)

sigma1 = matrix(2,2,2)
sigma1[1,2] = sigma1[2,1]=0.5
bvn1 = mvrnorm(100, mu=c(3,4), Sigma=sigma1)

sigma2 = matrix(1,2,2)
sigma2[1,2] = sigma2[2,1] = 0.5
bvn2 = mvrnorm(100, mu=c(7,8), Sigma=sigma2)

bvn1_average = apply(bvn1,2,mean)
bvn2_average = apply(bvn2,2,mean)

bvn1_cov = cov(bvn1)
bvn2_cov = cov(bvn2)

Let \(P(C_i): i=1,...k\) be the prior probabilities of the k classes. Given the training data \(X\), the probablity \(P(C_i)\) can be estimated by the proportion of points in the class \(C_i\)

The Bayes classifier is given by the posterior probability \(g_i(x) = logf(x|C_i) + log(C_i)\). We substitute the mean vector, covariance matrix, and prior probabilties with their estimates. The posterior probability of the class \(C_i\) is

\[g_i(x) = -\frac{1}{2}(x-\bar{X}_i)^TS_i^{-1}(x-\bar{X}_i)+\hat{P}(C_i)\]

The Bayes classification is that \(x\in C_i\) if \(g_i(x) > g_j(x)\) for \(i,j = 1,...,k\) and \(j\ne i\)

x = rbind(bvn1,bvn2)
g1 = -0.5*diag((x-bvn1_average)%*%solve(bvn1_cov)%*%t(x-bvn1_average))+0.5
g2 = -0.5*diag((x-bvn2_average)%*%solve(bvn2_cov)%*%t(x-bvn2_average))+0.5
print("first class")
which(g1>g2)
print("second class")
which(g1<g2)

print("two misclassified points")
x[which(g1[101:200]>g2[101:200]),]

[1] "first class"
  1. 1
  2. 2
  3. 3
  4. 4
  5. 5
  6. 6
  7. 7
  8. 8
  9. 9
  10. 10
  11. 11
  12. 12
  13. 13
  14. 14
  15. 15
  16. 16
  17. 17
  18. 18
  19. 19
  20. 20
  21. 21
  22. 22
  23. 23
  24. 24
  25. 25
  26. 26
  27. 27
  28. 28
  29. 29
  30. 30
  31. 31
  32. 32
  33. 33
  34. 34
  35. 35
  36. 36
  37. 37
  38. 38
  39. 39
  40. 40
  41. 41
  42. 42
  43. 43
  44. 44
  45. 45
  46. 46
  47. 47
  48. 48
  49. 49
  50. 50
  51. 51
  52. 52
  53. 53
  54. 54
  55. 55
  56. 56
  57. 57
  58. 58
  59. 59
  60. 60
  61. 61
  62. 62
  63. 63
  64. 64
  65. 65
  66. 66
  67. 67
  68. 68
  69. 69
  70. 70
  71. 71
  72. 72
  73. 73
  74. 74
  75. 75
  76. 76
  77. 77
  78. 78
  79. 79
  80. 80
  81. 81
  82. 82
  83. 83
  84. 84
  85. 85
  86. 86
  87. 87
  88. 88
  89. 89
  90. 90
  91. 92
  92. 94
  93. 95
  94. 96
  95. 97
  96. 98
  97. 99
  98. 100
  99. 126
  100. 133
  101. 140
  102. 146
  103. 166
  104. 170
  105. 172
  106. 180
[1] "second class"
  1. 91
  2. 93
  3. 101
  4. 102
  5. 103
  6. 104
  7. 105
  8. 106
  9. 107
  10. 108
  11. 109
  12. 110
  13. 111
  14. 112
  15. 113
  16. 114
  17. 115
  18. 116
  19. 117
  20. 118
  21. 119
  22. 120
  23. 121
  24. 122
  25. 123
  26. 124
  27. 125
  28. 127
  29. 128
  30. 129
  31. 130
  32. 131
  33. 132
  34. 134
  35. 135
  36. 136
  37. 137
  38. 138
  39. 139
  40. 141
  41. 142
  42. 143
  43. 144
  44. 145
  45. 147
  46. 148
  47. 149
  48. 150
  49. 151
  50. 152
  51. 153
  52. 154
  53. 155
  54. 156
  55. 157
  56. 158
  57. 159
  58. 160
  59. 161
  60. 162
  61. 163
  62. 164
  63. 165
  64. 167
  65. 168
  66. 169
  67. 171
  68. 173
  69. 174
  70. 175
  71. 176
  72. 177
  73. 178
  74. 179
  75. 181
  76. 182
  77. 183
  78. 184
  79. 185
  80. 186
  81. 187
  82. 188
  83. 189
  84. 190
  85. 191
  86. 192
  87. 193
  88. 194
  89. 195
  90. 196
  91. 197
  92. 198
  93. 199
  94. 200
[1] "two misclassified points"
A matrix: 8 × 2 of type dbl
4.2120894.406357
5.9868912.606797
3.4524282.750365
5.1753801.959169
3.2534164.969929
4.3986615.682706
1.9281653.643036
3.8565445.994505

Two classes have a common covariance matrix#

If two classes have a common covariance matrix \(S\), the posterior probability of the class \(C_i\) is

\[g_i(x) = -\frac{1}{2}(x-\bar{X}_i)^TS^{-1}(x-\bar{X}_i)+\hat{P}(C_i)\]

When \(g_i(x)\) is compared with \(g_j(x)\), the quadratic term \(x^TS^{-1}x\) cancels because it is common in all posterior probabilities of classes. Thus, it becomes a linear discriminant

\[g_i(x) = \bar{X}_i^TS^{-1}x -\frac{1}{2}\bar{X}_i^TS^{-1}\bar{X}_i + \hat{P}(C_i)\]

The Bayes classification is that \(x\in C_i\) if \(g_i(x) > g_j(x)\) for \(i,j = 1,...,k\) and \(j\ne i\)

pooldata = rbind(bvn1-mean(bvn1),bvn2-mean(bvn2))
bvn1_cov = bvn2_cov = cov(pooldata)

m1 = 0.5*bvn1_average%*%solve(bvn1_cov)%*%bvn1_average
m2 = 0.5*bvn2_average%*%solve(bvn1_cov)%*%bvn2_average

x = rbind(bvn1,bvn2)
g1 = bvn1_average%*%solve(bvn1_cov)%*%t(x) - c(m1,m1) + 0.5
g2 = bvn2_average%*%solve(bvn2_cov)%*%t(x) - c(m2,m2) + 0.5
print("first class")
which(g1>g2)
print("second class")
which(g1<g2)

print("two misclassified points")
print(x[which(g1[101:200]>g2[101:200]),])

[1] "first class"
  1. 2
  2. 3
  3. 4
  4. 5
  5. 6
  6. 7
  7. 8
  8. 9
  9. 10
  10. 11
  11. 12
  12. 13
  13. 15
  14. 16
  15. 17
  16. 19
  17. 20
  18. 21
  19. 22
  20. 23
  21. 24
  22. 26
  23. 27
  24. 28
  25. 29
  26. 30
  27. 31
  28. 32
  29. 33
  30. 34
  31. 35
  32. 36
  33. 37
  34. 38
  35. 39
  36. 40
  37. 41
  38. 42
  39. 43
  40. 44
  41. 45
  42. 46
  43. 47
  44. 48
  45. 49
  46. 50
  47. 51
  48. 52
  49. 53
  50. 54
  51. 55
  52. 56
  53. 57
  54. 58
  55. 59
  56. 60
  57. 61
  58. 62
  59. 63
  60. 64
  61. 65
  62. 66
  63. 67
  64. 68
  65. 69
  66. 70
  67. 71
  68. 72
  69. 73
  70. 74
  71. 75
  72. 76
  73. 77
  74. 78
  75. 79
  76. 80
  77. 81
  78. 82
  79. 83
  80. 84
  81. 85
  82. 86
  83. 87
  84. 88
  85. 89
  86. 90
  87. 92
  88. 94
  89. 95
  90. 96
  91. 97
  92. 98
  93. 99
  94. 100
  95. 163
  96. 170
  97. 172
[1] "second class"
  1. 1
  2. 14
  3. 18
  4. 25
  5. 91
  6. 93
  7. 101
  8. 102
  9. 103
  10. 104
  11. 105
  12. 106
  13. 107
  14. 108
  15. 109
  16. 110
  17. 111
  18. 112
  19. 113
  20. 114
  21. 115
  22. 116
  23. 117
  24. 118
  25. 119
  26. 120
  27. 121
  28. 122
  29. 123
  30. 124
  31. 125
  32. 126
  33. 127
  34. 128
  35. 129
  36. 130
  37. 131
  38. 132
  39. 133
  40. 134
  41. 135
  42. 136
  43. 137
  44. 138
  45. 139
  46. 140
  47. 141
  48. 142
  49. 143
  50. 144
  51. 145
  52. 146
  53. 147
  54. 148
  55. 149
  56. 150
  57. 151
  58. 152
  59. 153
  60. 154
  61. 155
  62. 156
  63. 157
  64. 158
  65. 159
  66. 160
  67. 161
  68. 162
  69. 164
  70. 165
  71. 166
  72. 167
  73. 168
  74. 169
  75. 171
  76. 173
  77. 174
  78. 175
  79. 176
  80. 177
  81. 178
  82. 179
  83. 180
  84. 181
  85. 182
  86. 183
  87. 184
  88. 185
  89. 186
  90. 187
  91. 188
  92. 189
  93. 190
  94. 191
  95. 192
  96. 193
  97. 194
  98. 195
  99. 196
  100. 197
  101. 198
  102. 199
  103. 200
[1] "two misclassified points"

         [,1]     [,2]
[1,] 4.104538 2.824454
[2,] 4.398661 5.682706
[3,] 1.928165 3.643036

Regularized discriminant analysis#

Let \(S_i\) be the sample covaraince matrix for class \(i\) and let \(S\) be the covariance matrix of the pool data. The covariance matrix is written as a weighted average of the three special cases

\[w(\lambda) = \lambda S + (1-\lambda) S_i\]
\[v(\lambda,\gamma) = (1-\gamma)w(\lambda) + \gamma\frac{1}{p}tr(w(\lambda))I\]

When \(\lambda=\gamma=0\), it is a quadratic classifier.

When \(\lambda=1\) and \(\gamma=0\), it is a linear classifier.

When \(\lambda=0\) and \(\gamma=1\), the covariance matrices are diagonal with \(\sigma^2\) and it is the nearest mean classifier.

When \(\lambda=1\) and \(\gamma=1\), the covariance matrices are diagonal with the same variance.

The choice of \(\lambda\) and \(\gamma\) can be optimized by cross-validation

library(mlbench)
library(caret)
library(glmnet)
library(klaR)

data(Sonar)
Sonar
Hide code cell output 
Loading required package: ggplot2

Loading required package: lattice

Loading required package: Matrix

Loaded glmnet 4.1-8
A data.frame: 208 × 61
V1V2V3V4V5V6V7V8V9V10⋯V52V53V54V55V56V57V58V59V60Class
<dbl><dbl><dbl><dbl><dbl><dbl><dbl><dbl><dbl><dbl>⋯<dbl><dbl><dbl><dbl><dbl><dbl><dbl><dbl><dbl><fct>
10.02000.03710.04280.02070.09540.09860.15390.16010.31090.2111⋯0.00270.00650.01590.00720.01670.01800.00840.00900.0032R
20.04530.05230.08430.06890.11830.25830.21560.34810.33370.2872⋯0.00840.00890.00480.00940.01910.01400.00490.00520.0044R
30.02620.05820.10990.10830.09740.22800.24310.37710.55980.6194⋯0.02320.01660.00950.01800.02440.03160.01640.00950.0078R
40.01000.01710.06230.02050.02050.03680.10980.12760.05980.1264⋯0.01210.00360.01500.00850.00730.00500.00440.00400.0117R
50.07620.06660.04810.03940.05900.06490.12090.24670.35640.4459⋯0.00310.00540.01050.01100.00150.00720.00480.01070.0094R
60.02860.04530.02770.01740.03840.09900.12010.18330.21050.3039⋯0.00450.00140.00380.00130.00890.00570.00270.00510.0062R
70.03170.09560.13210.14080.16740.17100.07310.14010.20830.3513⋯0.02010.02480.01310.00700.01380.00920.01430.00360.0103R
80.05190.05480.08420.03190.11580.09220.10270.06130.14650.2838⋯0.00810.01200.00450.01210.00970.00850.00470.00480.0053R
90.02230.03750.04840.04750.06470.05910.07530.00980.06840.1487⋯0.01450.01280.01450.00580.00490.00650.00930.00590.0022R
100.01640.01730.03470.00700.01870.06710.10560.06970.09620.0251⋯0.00900.02230.01790.00840.00680.00320.00350.00560.0040R
110.00390.00630.01520.03360.03100.02840.03960.02720.03230.0452⋯0.00620.01200.00520.00560.00930.00420.00030.00530.0036R
120.01230.03090.01690.03130.03580.01020.01820.05790.11220.0835⋯0.01330.02650.02240.00740.01180.00260.00920.00090.0044R
130.00790.00860.00550.02500.03440.05460.05280.09580.10090.1240⋯0.01760.01270.00880.00980.00190.00590.00580.00590.0032R
140.00900.00620.02530.04890.11970.15890.13920.09870.09550.1895⋯0.00590.00950.01940.00800.01520.01580.00530.01890.0102R
150.01240.04330.06040.04490.05970.03550.05310.03430.10520.2120⋯0.00830.00570.01740.01880.00540.01140.01960.01470.0062R
160.02980.06150.06500.09210.16150.22940.21760.20330.14590.0852⋯0.00310.01530.00710.02120.00760.01520.00490.02000.0073R
170.03520.01160.01910.04690.07370.11850.16830.15410.14660.2912⋯0.03460.01580.01540.01090.00480.00950.00150.00730.0067R
180.01920.06070.03780.07740.13880.08090.05680.02190.10370.1186⋯0.03310.01310.01200.01080.00240.00450.00370.01120.0075R
190.02700.00920.01450.02780.04120.07570.10260.11380.07940.1520⋯0.00840.00100.00180.00680.00390.01200.01320.00700.0088R
200.01260.01490.06410.17320.25650.25590.29470.41100.49830.5920⋯0.00920.00350.00980.01210.00060.01810.00940.01160.0063R
210.04730.05090.08190.12520.17830.30700.30080.23620.38300.3759⋯0.01930.01180.00640.00420.00540.00490.00820.00280.0027R
220.06640.05750.08420.03720.04580.07710.07710.11300.23530.1838⋯0.01410.01900.00430.00360.00260.00240.01620.01090.0079R
230.00990.04840.02990.02970.06520.10770.23630.23850.00750.1882⋯0.01730.01490.01150.02020.01390.00290.01600.01060.0134R
240.01150.01500.01360.00760.02110.10580.10230.04400.09310.0734⋯0.00910.00160.00840.00640.00260.00290.00370.00700.0041R
250.02930.06440.03900.01730.04760.08160.09930.03150.07360.0860⋯0.00350.00520.00830.00780.00750.01050.01600.00950.0011R
260.02010.00260.01380.00620.01330.01510.05410.02100.05050.1097⋯0.01080.00700.00630.00300.00110.00070.00240.00570.0044R
270.01510.03200.05990.10500.11630.17340.16790.11190.08890.1205⋯0.00610.00150.00840.01280.00540.00110.00190.00230.0062R
280.01770.03000.02880.03940.06300.05260.06880.06330.06240.0613⋯0.01020.01220.00440.00750.01240.00990.00570.00320.0019R
290.01000.02750.01900.03710.04160.02010.03140.06510.18960.2668⋯0.00880.01040.00360.00880.00470.01170.00200.00910.0058R
300.01890.03080.01970.06220.00800.07890.14400.14510.17890.2522⋯0.00380.00960.01420.01900.01400.00990.00920.00520.0075R
⋮⋮⋮⋮⋮⋮⋮⋮⋮⋮⋮⋱⋮⋮⋮⋮⋮⋮⋮⋮⋮⋮
1790.01970.03940.03840.00760.02510.06290.07470.05780.13570.1695⋯0.01340.00970.00420.00580.00720.00410.00450.00470.0054M
1800.03940.04200.04460.05510.05970.14160.09560.08020.16180.2558⋯0.01460.00400.01140.00320.00620.01010.00680.00530.0087M
1810.03100.02210.04330.01910.09640.18270.11060.17020.28040.4432⋯0.02040.00590.00530.00790.00370.00150.00560.00670.0054M
1820.04230.03210.07090.01080.10700.09730.09610.13230.24620.2696⋯0.01760.00350.00930.01210.00750.00560.00210.00430.0017M
1830.00950.03080.05390.04110.06130.10390.10160.13940.25920.3745⋯0.01810.00190.01020.01330.00400.00420.00300.00310.0033M
1840.00960.04040.06820.06880.08870.09320.09550.21400.25460.2952⋯0.02370.00780.01440.01700.00120.01090.00360.00430.0018M
1850.02690.03830.05050.07070.13130.21030.22630.25240.35950.5915⋯0.01670.01990.01450.00810.00450.00430.00270.00550.0057M
1860.03400.06250.03810.02570.04410.10270.12870.18500.26470.4117⋯0.01410.00190.00670.00990.00420.00570.00510.00330.0058M
1870.02090.01910.04110.03210.06980.15790.14380.14020.30480.3914⋯0.00780.02010.01040.00390.00310.00620.00870.00700.0042M
1880.03680.02790.01030.05660.07590.06790.09700.14730.21640.2544⋯0.01050.00240.00180.00570.00920.00090.00860.01100.0052M
1890.00890.02740.02480.02370.02240.08450.14880.12240.15690.2119⋯0.00960.01030.00930.00250.00440.00210.00690.00600.0018M
1900.01580.02390.01500.04940.09880.14250.14630.12190.16970.1923⋯0.01210.01080.00570.00280.00790.00340.00460.00220.0021M
1910.01560.02100.02820.05960.04620.07790.13650.07800.10380.1567⋯0.01500.00600.00820.00910.00380.00560.00560.00480.0024M
1920.03150.02520.01670.04790.09020.10570.10240.12090.12410.1533⋯0.01080.00620.00440.00720.00070.00540.00350.00010.0055M
1930.00560.02670.02210.05610.09360.11460.07060.09960.16730.1859⋯0.00720.00550.00740.00680.00840.00370.00240.00340.0007M
1940.02030.01210.03800.01280.05370.08740.10210.08520.11360.1747⋯0.01340.00940.00470.00450.00420.00280.00360.00130.0016M
1950.03920.01080.02670.02570.04100.04910.10530.16900.21050.2471⋯0.00830.00800.00260.00790.00420.00710.00440.00220.0014M
1960.01290.01410.03090.03750.07670.07870.06620.11080.17770.2245⋯0.01240.00930.00720.00190.00270.00540.00170.00240.0029M
1970.00500.00170.02700.04500.09580.08300.08790.12200.19770.2282⋯0.01650.00560.00100.00270.00620.00240.00630.00170.0028M
1980.03660.04210.05040.02500.05960.02520.09580.09910.14190.1847⋯0.01320.00270.00220.00590.00160.00250.00170.00270.0027M
1990.02380.03180.04220.03990.07880.07660.08810.11430.15940.2048⋯0.00960.00710.00840.00380.00260.00280.00130.00350.0060M
2000.01160.07440.03670.02250.00760.05450.11100.10690.17080.2271⋯0.01410.01030.01000.00340.00260.00370.00440.00570.0035M
2010.01310.03870.03290.00780.07210.13410.16260.19020.26100.3193⋯0.01500.00760.00320.00370.00710.00400.00090.00150.0085M
2020.03350.02580.03980.05700.05290.10910.17090.16840.18650.2660⋯0.01200.00390.00530.00620.00460.00450.00220.00050.0031M
2030.02720.03780.04880.08480.11270.11030.13490.23370.31130.3997⋯0.00910.00450.00430.00430.00980.00540.00510.00650.0103M
2040.01870.03460.01680.01770.03930.16300.20280.16940.23280.2684⋯0.01160.00980.01990.00330.01010.00650.01150.01930.0157M
2050.03230.01010.02980.05640.07600.09580.09900.10180.10300.2154⋯0.00610.00930.01350.00630.00630.00340.00320.00620.0067M
2060.05220.04370.01800.02920.03510.11710.12570.11780.12580.2529⋯0.01600.00290.00510.00620.00890.01400.01380.00770.0031M
2070.03030.03530.04900.06080.01670.13540.14650.11230.19450.2354⋯0.00860.00460.01260.00360.00350.00340.00790.00360.0048M
2080.02600.03630.01360.02720.02140.03380.06550.14000.18430.2354⋯0.01460.01290.00470.00390.00610.00400.00360.00610.0115M

Regularized Discriminant Analysis

set.seed(1337)
cv_5_grid = trainControl(method = "cv", number = 5)

fit_rda_grid = train(Class ~ ., data = Sonar, method = "rda", trControl = cv_5_grid)
fit_rda_grid

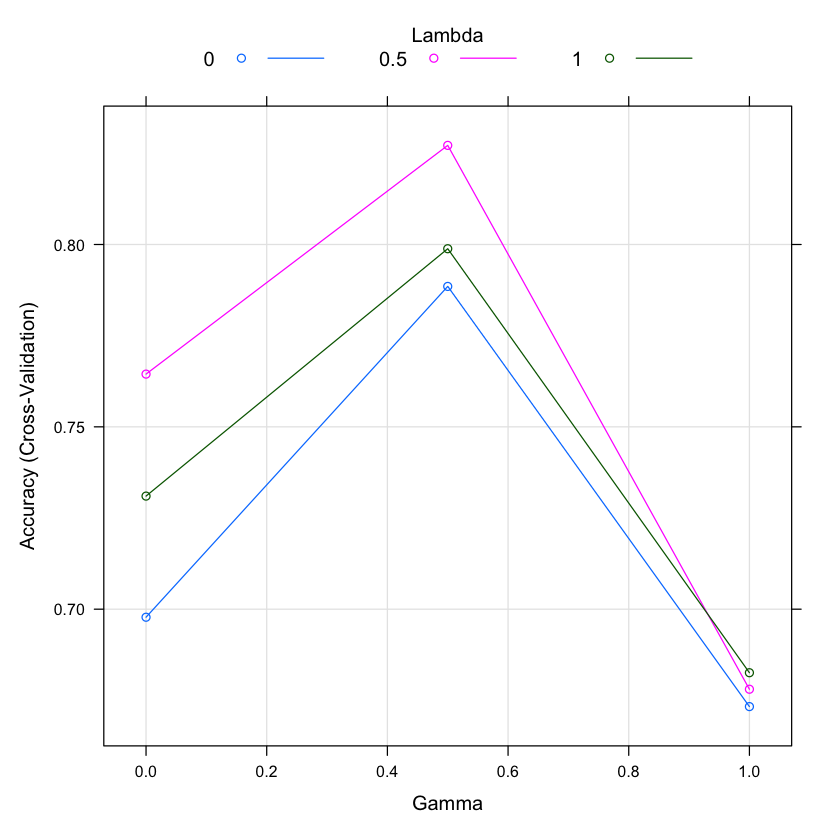
plot(fit_rda_grid)

Regularized Discriminant Analysis 

208 samples
 60 predictor
  2 classes: 'M', 'R' 

No pre-processing
Resampling: Cross-Validated (5 fold) 
Summary of sample sizes: 167, 166, 166, 167, 166 
Resampling results across tuning parameters:

  gamma  lambda  Accuracy   Kappa    
  0.0    0.0     0.6977933  0.3791172
  0.0    0.5     0.7644599  0.5259800
  0.0    1.0     0.7310105  0.4577198
  0.5    0.0     0.7885017  0.5730052
  0.5    0.5     0.8271777  0.6502693
  0.5    1.0     0.7988386  0.5939209
  1.0    0.0     0.6732869  0.3418352
  1.0    0.5     0.6780488  0.3527778
  1.0    1.0     0.6825784  0.3631626

Accuracy was used to select the optimal model using the largest value.
The final values used for the model were gamma = 0.5 and lambda = 0.5.
_images/3b05f8bd136192d283c39d360fc59ae91ef8263b68d35b3017647b2bf8185469.png